一 为什么不使用主键自增，一定是绝对的吗？

要回答上面的问题，我们需要先了解一下一下三点内容：

  1. 大表为什么不适用自增？
  2. UUID是好的替代方案吗？
  3. 什么是雪花算法？

二 大表为什么不使用自增主键？

我们假设一个大表分片场景，如下图：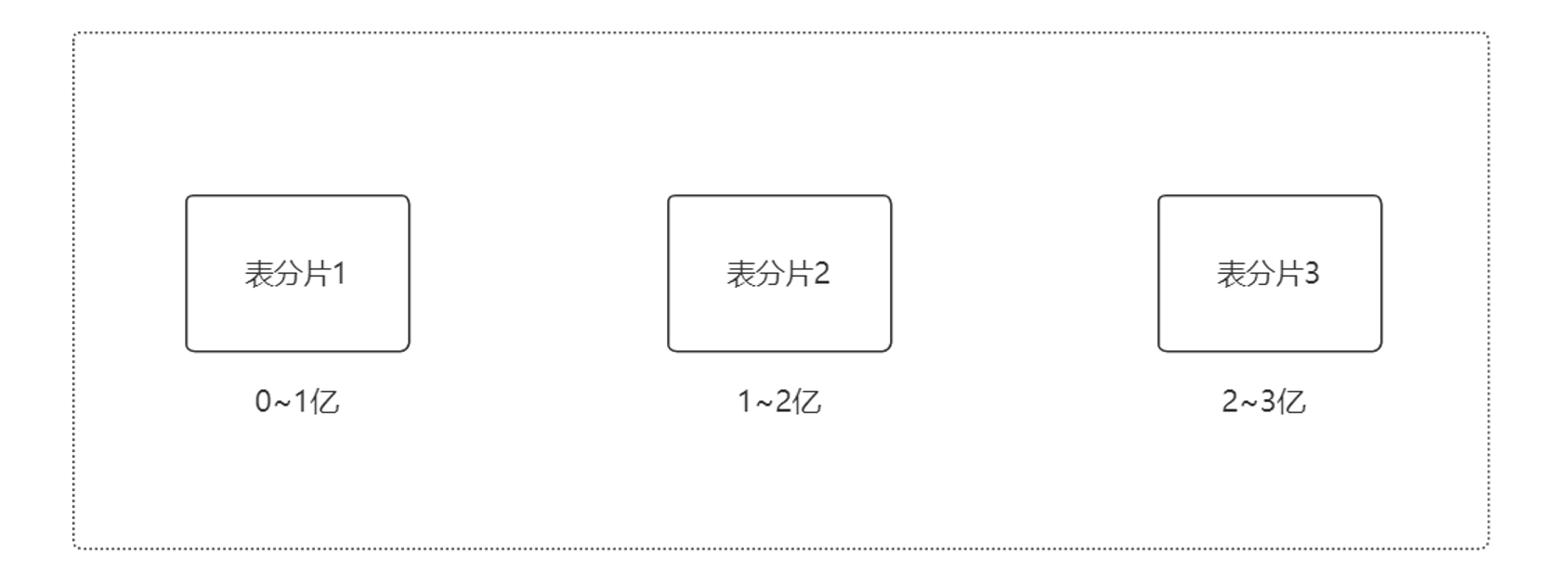

考虑几个问题：

  1. 表范围如何确定？
  2. 如何更改某分片的范围？

由于以上两个问题，自增的一些问题就产生了：

  1. 自增是连续的
  2. 只能采用范围分片
  3. 产生尾部热点效应（即我们后更新的数据肯定存在于范围靠后的分片，即其实压力大多集中在最后的分片）

三 UUID是好的替代方案吗？

答案： 否！

众所周知，UUID有以下几个特性：

1. UUID是完全无序的
2. UUID占用空间大

以上两个特点，我们从数据库底层开始讲起，起必然会引起如下的问题：

1. 大量的索引重排
2. 页决裂/分裂
3. 太长，空间浪费（相较于整型，长整型）

什么是索引重排？

常规的自增id，数据库底层在构造B+树的时候，会逐个在尾部进行接入，重新计算树，但是UUID的无序会导致并非每次都在最后，会插入树的随机位置，断裂树的结构，例如我100万次的插入，却插入了第2个位置，那么从2开始后续所有的节点全部重新排列一遍，非常的消耗性能。

什么是页分裂？

后续详细补充。

四 什么是雪花算法？

Twitter设计的以时间为基准的Id。

如上所示，一毫秒雪花能生存400万的id，在绝大多数情况下，都是够用的。

注意： 注意时间回拨带来的影响。